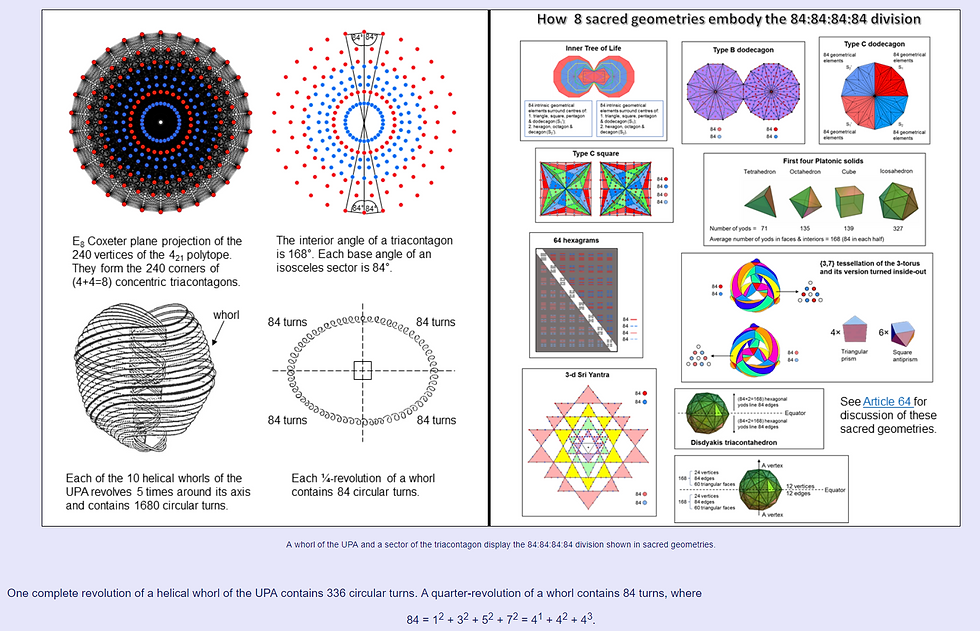
This 84:84:84:84 pattern appears in:
1. the inner Tree of Life, as the 84 geometrical elements that are intrinsic to it and surround the centres of 4 sets of polygons:
the triangle, square, pentagon & dodecagon in either half; the hexagon, octagon & decagon in either half.
2. the 84 red yods and 84 blue yods that surround the centres of each Type B dodecagon.
3. The 84 geometrical elements in each quadrant of the Type C dodecagon. This is because the number of geometrical elements surround the centre of a Type C n-gon = 28n, so that three sectors have 84 such geometrical elements and the 12 sectors of the dodecagon have 4×84 geometrical elements.
4. Surrounding the centre of a Type C n-gon are 42n yods. A pair of Type C squares (n = 4) has 84 yods per quadrant.
5. Joining the vertices of the Platonic solids to their centres creates internal triangles. When their faces are divided into sectors and all triangles turned into tetractyses, the first 4 Platonic solids have 672 yods. On average, each solid has 168 yods, 84 in each half.
6. On either side of the diagonal of the 8×8 array of 64 hexagrams are 28 hexagrams with 168 lines & broken lines. 84 of them are lines (Yang) and 84 are broken lines (Yin).
7. The {3,7} tessellation of the hyperbolic surface of the 3-torus needs 56 triangles. This can be achieved by sticking the square faces of 4 triangular prisms with 8 triangular faces to the square faces of 6 square antiprisms with 48 triangular faces. Turning the 56 hyperbolic triangles into tetractyses generates 168 hexagonal yods lining sides as 84 pairs. 84 pairs of hexagonal yods line the sides of tetractyses tiling a version of the 3-torus that is turned inside out, so that the 112 tetractyses in both 3-tori are lined by 4 sets of 84 hexagonal yods.
8. Turning into tetractyses the 42 triangles surrounding the centre of the 3-dimensional Sri Yantra generates 336 yods that line their 126 sides. The six hexagonal yods on the sides of each tetractys form two intersecting triangular arrays of 3 yods. Each tetractys has two independent corners, one being associated with one set of 3 hexagonal yods and the other being associated with the second set of 3 hexagonal yods. The 21 tetractyses in each half of the Sri Yantra consist of two sets of 4 yods, i.e., each half comprises two sets of (21×4=84) yods.
9. The disdyakis triacontahedron has three types of vertices: A, B & C. When it is orientated so that the axis passing through two diametrically opposite A vertices is vertical, the equatorial plane of the disdyakis triacontahedron contains 12 vertices and edges, 84 edges are above this plane and 84 edges are below it. Turning the 120 faces into tetractyses generates 336 hexagonal lining edges that are either above or below this plane (84 pairs in each half).
10. Surrounding the axis above the equator are 84 edges, 24 vertices & 60 triangular faces, i.e, 84 vertices & triangles. Similarly for below the equator. Two sets of 84 geometrical elements surround the axis in each half of the polyhedron.