SUPERSTRING THEORY

SUPERSTRING THEORY

There are:

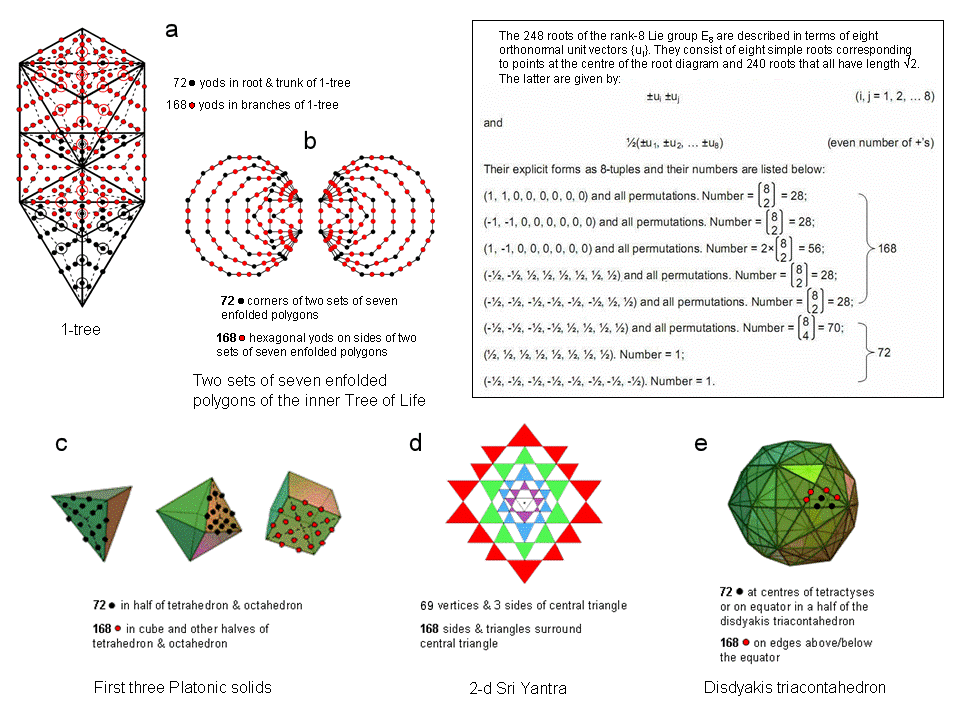
1. 240 yods other than Sephiroth in the 1-tree constructed from Type A triangles (see a). They comprise the 72 yods in its trunk & root (see here for their definition) and 168 yods in its branches;
2. 240 yods on the boundaries of the two separate sets of the seven enfolded polygons (see (b)). They comprise 72 black yods at corners and 168 red hexagonal yods (see here for further discussion);
3. 240 hexagonal yods on the faces of the first three Platonic solids whose sectors are tetractyses (see (c)). They comprise 72 black yods in the faces of half the tetrahedron and half the octahedron and 168 red yods in their remaining faces (see here for further discussion);
4. 240 vertices, sides & triangles surrounding the centre of the 2-dimensional Sri Yantra (see (d)). They comprise 69 vertices and the three sides of the central triangle, i.e., 72 geometrical elements, and 168 sides & triangles that surround the central triangle (see here for further discussion);
5. 240 hexagonal yods in the 60 faces in each half of the disdyakis triacontahedron when each face is a tetractys (see (e)). They comprise 72 black hexagonal yods, which are either at centres of tetractyses or on the equator when its plane is perpendicular to an axis passing through two diametrically opposite A vertices, and 168 red hexagonal yods on the 84 edges either above or below the equator (see here for further discussion).

These analogies between the properties of five sacred geometries exist because they are all equivalent representations of the cosmic blueprint that embodies the divine archetypes. This blueprint manifests in the subatomic world as the UPA, the subquark state of the E8×E8 heterotic superstring. Article 53 discusses the correspondences in more detail.
When regarded as separate from each other, the outer and inner forms of the Tree of Life are composed of 426 triangles with 248 corners (74 in its outer form and 174 in its inner form). Eight corners (denoted by white yods) are either shared between the outer and inner forms or have — as their projections onto the plane of the enfolded polygons — the two endpoints of the root edge of the latter. This leaves 240 corners which are unshared. There are (74−2=72) unshared corners in the outer Tree of Life and (174−6=168) unshared corners in the inner Tree of Life. The 240 unshared corners in the separate outer and inner forms of the Tree of Life denote the 240 roots of E8 and the 72 corners in the outer Tree unshared with those in the inner Tree denote the 72 roots of E6.

In all these sacred geometries, the number 72 plays the more fundamental role in marking out in each case the skeletal foundation, whilst the number 168 "fleshes out", so to speak, the complete form of the geometrical object.

E8XE8 SUPERSTRING THEORY

The Tetrad Principle discussed in Article 1 states that the fourth member of a class of mathematical objects embodies numbers of universal (and therefore scientific) significance. As the hexagon is the fourth type of regular polygon and the fourth of the seven regular polygons making up the inner form of the Tree of Life, it should not be surprising that the pair of joined hexagons embodies parameters of the Tree of Life. For example, when their 12 sectors are tetractyses, they contain 70 yods (10 corners & 60 other yods). They correspond to the 10 Sephiroth of the Tree of Life and its 60 hexagonal yods when its 16 triangles become tetractyses. The Type C hexagon is the fourth class of hexagon:

hexagon → Type A → Type B → Type C → etc.

A Type C n-gon has (42n+1) yods. A Type C hexagon (n=6) has 253 yods. Two joined Type C hexagons have 502 yods. 500 (=50×10) yods surround their centres, showing how ELOHIM, the Godname of Binah with number value 50, prescribes this particular pair of hexagons. Outside the four black yods in their shared edge are 496 yods. This is the gematria number of Malkuth, the last Sephirah of the Tree of Life, signifying on a cosmic scale the physical universe (the space-time continuum):
400 6 20 30 40=496
248 such yods belong to each hexagon, where 248 is the number value of Raziel, the Archangel of Chokmah. They symbolize the sets of 248 roots of E8 and E8′ in the heterotic gauge symmetry group E8×E8′.

The following correspondences exist:

two white yods → two of the eight simple roots of E8 (E8′) that are not roots of E6 (E6′), its rank-6, exceptional subgroup.
six yellow yods → six simple roots of E6 (E6′).
72 red yods → 72 roots of E6 (E6′).
168 blue yods → 168 roots of E8 (E8′) that are not roots of E6 (E6′).
An alternative interpretation
As the topmost corner of each hexagon coincides with the bottom corner of its counterpart enfolded in the next higher Tree of Life, there are 500 (=50×10) yods that are intrinsic to each pair of hexagons enfolded in any Tree. This shows how ELOHIM, the Godname of Binah with number 50, prescribes these hexagons. Their top & bottom corners and their centres are located at the positions of the Sephiroth on the Pillars of Mercy and Judgement. The number of yods intrinsic to the two hexagons = 502 – 6 = 496. 248 such yods are associated with each hexagon. For the hexagon on the right of the root edge, they comprise two black yods on the root edge, six yellow centres of sectors, 72 red yods that are either hexagonal yods at centres of tetractyses or their corners and 168 blue yods that are either hexagon yods on sides of tetractyses or the two corners on the right-hand side of the hexagon. For the hexagon on the left, the 248 yods comprise a similar set of yods. The 496 yods intrinsic to the two hexagons symbolize the two sets of 248 roots of E8 in the heterotic gauge symmetry group E8×E8′.

The hexagon can be regarded as Nature's primary polygon, manifesting, for example, in the molecule of benzene, the basic building block of the aromatic hydrocarbon compounds, graphite and the honeycombs of bees. Perhaps its most remarkable and fundamental property is that discussed here, namely, its embodiment of the dimension 248 of the gauge symmetry group E8 governing the forces between one of the two types of heterotic superstring.

Article 60 and #39 at Superstrings as sacred geometry/Tree of Life discuss how the 496 roots of E8×E8′ manifest in the inner Tree of Life when its polygons are Type C.

THE INNER TREE OF LIFE ENCODES THE TEN TREES OF LIFE MAPPING THE TEN DIMENSIONS OF SUPERSTRING SPACE-TIME

Ten overlapping Trees of Life have 520 yods when their 124 triangles are turned into tetractyses.∗ This is the number of yods outside the shared root edge of the (7+7) enfolded polygons. The inner Tree of Life encodes the ten-fold development of the outer Tree of Life. The ten Trees of Life map the ten dimensions of superstring space-time. The inner Tree of Life is like the DNA molecule in a cell: just as DNA determines the self-replication of the latter, so the inner Tree encodes the complete transformation of each Sephirah in the outer Tree of Life into a Tree, so that a single Tree becomes ten Trees.

∗Proof: The number of yods in n overlapping Trees of Life when their (12n+4) triangles with (6n+4) corners and (16n+6) sides are tetractyses ≡ Y(n) = 6n + 4 + 2(16n+6) + 12n + 4 = 50n + 20. Therefore, Y(10) = 520. The seven separate polygons have 295 yods (see here). When they become enfolded in one another, the four yods in each of seven sides become the four yods of their shared root edge. The right-hand corner of the triangle coincides with the centre of the hexagon, the right-hand corner of the pentagon becomes the centre of the decagon, two hexagonal yods on each sloping side of the triangle coincide with hexagonal yods on corresponding sides of a sector of the hexagon and the centre of the triangle coincides with the hexagonal yod at the centre of this sector. The number of yods in the seven enfolded polygons = 295 − 6×4 − 1 − 1 − 2×2 − 1 = 295 − 31 = 264. Outside the root edge are (264−4=260) yods in the seven enfolded polygons and (2×260=520) yods in the (7+7) enfolded polygons.

THE ENCODINGS OF E8×E8 IN 10 TREES OF LIFE & IN THE INNER TREE OF LIFE

We saw in #24 that the 520 yods outside the root edge of the (7+7) enfolded polygons correspond to the 520 yods in 10 overlapping Trees of Life. Each Tree represents one of the 10 dimensions of the space-time of superstrings. The 496 spin-1 particles that transmit their forces are symbolized by the 496 yods up to (but not including) Chesed of the tenth Tree. There are 248 yods up to Chesed of the fifth Tree (the 31st SL). They symbolize the 248 spin-1 particles that transmit the forces between superstrings of ordinary matter governed by the first of the two E8 Lie groups in E8×E8. The remaining 248 blue yods above the 31st SL symbolize the 248 particles that transmit the forces between superstrings of shadow matter governed by the second E8 group. The lowest Tree has 80 yods, where 80 is the number of Yesod. They comprise 13 turquoice yods down to the Path between Chokmah and Binah and 67 violet yods below this Path, where 67 is the number value of Binah. Above the 1-tree are 168 red yods up to Chesed of the fifth Tree. This 80:168 division of the dimension 248 of E8 is a characteristic feature of holistic systems embodying this number (see The holistic pattern).

As one corner of each triangle coincides with the centre of a hexagon and as one corner of each pentagon coincides with the centre of a decagon, only five of each set of seven polygons have centres that are not also corners of polygons. The (7+7) enfolded polygons have 524 yods. (524−5−5=514) yods surround these ten white centres.The 14 enfolded polygons lie in the plane containing the side pillars of the outer Tree of Life. The latter has 70 yods, of which seven coloured black lie on each side pillar, leaving 60 green yods. The number of yods in the (7+7) enfolded polygons that surround the ten pure centres and which are unshared with the outer Tree = 514 − 7 − 7 = 500 = 50×10. ELOHIM, the Godname of Binah with number value 50, prescribes those yods intrinsic to the inner Tree of Life that surround centres of its polygons. Four yods lie in the root edge, so that (500−4=496) intrinsic yods outside the root edge surround the ten centres. Each set of seven enfolded polygons contains 248 such yods. This is how the inner Tree of Life encodes the root composition of E8×E8, one of the two symmetry groups governing the forces between heterotic superstrings. The factor group arises from the two mirror-image halves of the 14 enfolded polygons of the inner Tree of Life.

The following table shows the numbers of intrinsic yods outside the root edge that surround the centres of each enfolded polygon:
A ("m+n" means that the polygon has m hexagonal yods at the centres of its sectors and n hexagonal yods on their sides).

The first four enfolded polygons have 80 yods that correspond to the 80 yods in the 1-tree and the last three enfolded polygons have 168 yods that correspond to the 168 red yods above them up to the 31st SL. The 80:168 division appears naturally in the seven enfolded polygons. Moreover, the division of the 80 yods into the 13 turquoice yods and the 67 violet yods appears in the first four enfolded polygons, the triangle having 13 turquoice yods (all hexagonal yods) and the square, pentagon & hexagon having 67 violet yods. Notice also that the 248 intrinsic yods surrounding the five independent centres consist of 31 corners of polygons and 217 hexagonal yods. This compares with the 31 SLs (that is, 31 corners of tetractyses) and the 217 hexagonal yods up to Chesed of the fifth Tree. It is highly implausible that such a degree of correlation between two objects claimed to embody the group-theoretical number 248 could be due to chance. Instead, it is powerful evidence that they are isomorphic, sacred-geometrical embeddings of this archetypal number.

According to the table, the enfolded decagon and dodecagon have (38+46=84) hexagonal yods on the sides of their 22 tetractyses, leaving 84 yods in the octagon and in these two polygons. This 84:84 division is characteristic of holistic systems that embody the number 168 (see The holistic pattern). As explained in many other discussions, it physically manifests as the 840:840 division of circular turns in the outer and inner 2½ spirals made by each helical whorl of the UPA/subquark superstring as it winds around its axis of spin. Every half-revolution of a helical whorl contains 168 turns and every quarter-revolution contains 84 turns.

HOW POLYGONAL NUMBERS & SACRED GEOMETRIES REPRESENT THE SUPERSTRING STRUCTURAL PARAMETER 3360

a) The first seven orders of the first 10 types of polygonal numbers can be assigned to the seven hexagonal yods in the 10 1st-order tetractyses making up the 2nd-order tetractys. Their sum is 3360 (see here). This is the number of yods in the seven enfolded polygons of the inner Tree of Life when their sectors are 2nd-order tetractyses (for proof, see Article 24, ref. 3);

b) The 62 vertices of the disdyakis triacontahedron can fit 28 Platonic and Catalan solids. They consist of ten tetrahedra, five cubes, five octahedra, five rhombic dodecahedra, one icosahedron, one dodecahedron and one rhombic triacontahedron. Turning the sectors of their faces into tetractyses generates 3360 hexagonal yods;

c) The first (6+6) enfolded polygons of the inner Tree of Life constitutes a holistic subset of the (7+7) enfolded polygons of the inner Tree of Life. When their 70 sectors are turned into tetractyses, the first (6+6) enfolded polygons have 336 yods other than their 50 corners. The 120 polygons enfolded in 10 overlapping Trees of Life have 3360 yods other than their corners (see also here);

d) There are 336 corners, sides & triangles outside the root edge of the (7+7) enfolded polygons that are intrinsic to them in the sense that none of these geometrical elements belong also to the triangles making up the outer form of the Tree of Life. The 140 polygons that are enfolded in 10 overlapping Trees of Life have 3360 such geometrical elements unshared with these Trees (see also here).

The 2nd-order tetractys array of 70 polygonal numbers is the arithmetic counterpart of these four sacred geometrical representations of the superstring structural parameter 3360 — the number of circular turns in one complete revolution of the ten helical whorls of the spin-½ UPA/subquark superstring around its axis of spin. Demonstrated here is the beautiful harmony between number and sacred geometry expressed through the template of the 2nd-order tetractys. It is discussed in detail in (8) at Polygonal numbers.

POLYGONAL NUMBERS SUPERSTRING AND (64 TETRAHEDRON GRID(E8(XEN PARTICLE)))

polygonal numbers and 28