Numbers Magick
- Dimensional consciousness(LC)

- Dec 17, 2017
- 12 min read
The ancients claimed that God works by mathematics. Their religion was a conglomeration of religion, astrology, alchemy, physical and mental science, and mathematics. Ancient astrology divided the starry heavens into 36 constellations. These were represented by different amulets called “Sigilla Solis,” or the sun seal. These amulets were worn by the pagan priests, and they contained all the numbers from 1 to 36. God Works by Numbers: Science, and particularly geometry and astronomy, was linked directly to the divine for ancient builders of temples and monuments. Since God created the universe after geometric and harmonic principles, to seek these principles was therefore to seek and worship God. 666 and the Magickal Seal of the Sun: The “Seals of the Planets,” popular before the time of Christ according to Budge (Amulets and Superstitions), are interesting because the seal containing “the Grand Number of the Sun” contains the very sacred number 36 laid out in a 6×6 square with the numbers from 1 to 36 so arranged that they add up the same in all directions, with the total of the whole seal 666. Though popular also in Eastern lands, the Greek and Roman, or Latin, inscriptions on these seals show also their popularity in the West.. Since the sun-god was considered as the ruler over the 36 constellations of the sky and the 36 rooms of the circle of the zodiac, it was inevitable that the summary number of the numbers from 1 to 36, the number 666 should have been assigned to the sun as the ruler over all the gods of heaven and earth. Babylonian astrologers divided the starry heavens into 36 constellations (ten days each). Adding the numbers of any column either horizontally or vertically, and also the two diagonals crossing the square, the total is the same — 111. The sum of the six columns, either horizontally or vertically, is 666. The illustrations below taken from actual amulets in the Berlin Museum
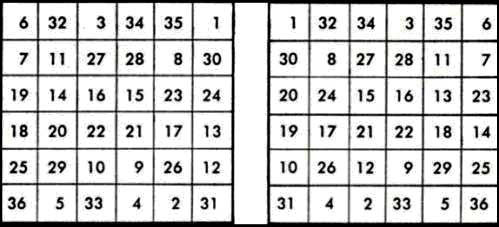
The 6×6 Magic Square of the Sun contains the first 36 numbers arranged in such a fashion so that each line of numbers, weather added horizontally, vertically or diagonally from corner to corner, will yield the “solar number” 111. The entire magic square therefore equals 666, a number which was significant to early Christian mystics. In Hebrew Kabbalah, the names of the intelligence of the Sun and Spirit of the Sun were designed to equal 111 and 666 respectively. Like 888, 666 is an important musical number, for .666 is the ration of the perfect fifth, the most powerful harmonic interval.

The second illustration is also a solar seal, but it honors the star Basilisco, which was the diminutive form of the Greek basileus (king), thus meaning the same as the Latin “regulus”. Now, Regulus is the only first-magnitude star in the constellation of Leo. The sun and the moon are again clearly seen on this amulet, and on the reverse side is the same arrangement of numerals, with the actual figure given of the total 666 The lower coin shows the conjunction of the Sun, Moon and the star Regulus in the constellation of Leo the Lion that occurred on 19 August 1705 Table #1 as illustrated above is also referred to in numerology as the magic Square of the Sun. There are similar magic squares for Saturn, Jupiter, Mars, Venus, Mercury and the Moon, all of which have been known for centuries
This ‘magic square of the sun’ is associated with the ‘The Philosophers stone:
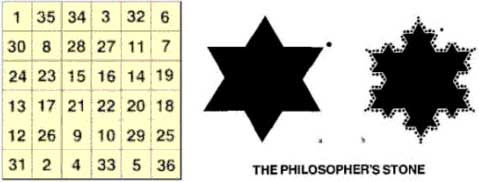
Infinite star tetrahedron fractal

Circle – infinite – spirit, etc aspects.
Square – finite, universe, material, physical, body, etc aspects.
Triangle – Trinity, Unity aspects, bridge between two, getting to three from two and back to one.
The Philosopher’s stone is associated with the hexagram(star tetrahedron)…a symbol that comes up over and over again in connection with the number 666 The Hexagram of Earth represents the Solar energy that makes concrete matter that we can move and touch, in short, The Philosophers Stone The double triangle viewed by the Jewish Kabbalists as Solomon’s Seal is…the Sri–Antana of the Archaic Aryan Temple, the Mystery of Mysteries, a geometrical synthesis of the whole occult doctrine. The two interlaced triangles are the Buddham-Gums of Creation. They contain the ‘squaring of the Circle,’ the ‘Philosophers’ Stone,’ the great problems of Life and Death–the mystery of Evil.
The Babylonians, who invented the zodiac, considered each of the twelve signs to rule over the twelve months of the year. They further divided each of the 12 houses into 3 rooms. 12 x 3 = 36. Each of the 36 designated gods ruled over his own 10 degrees of the 360 zodiac and over his 10 days of the 360-day zodiacal year. It was believed that no god would strike you if you were wearing his identifying amulet. It would thus behoove you to invoke the numbers of each of the gods. The number which encompasses them all is 666. An amulet which contained all of these numbers would insure the favor of all the gods, anywhere, anytime. But the ancients didn’t stop with using magic numbers in serial order. Arranging these numbers in a magic square could greatly compound their power

Each line, column or diagonal adds up to 111. The sum of the six lines or six columns is 666. With the numbers arranged thus in magic squares, you can hope to invoke the full power of the sun, the king of the gods. His number is 666. (See bottom for coins and illustrations from the book.) Quite obviously, the “666” has existed in religions since ancient antiquity. So we must then inquire as to how this came to mean so much. In ancient religions, Gods had a triple aspect to them, which was the creator, the maintainer, and the destroyer Sacred Tetractys: The Pythagoreans adored numbers. Aristotle, in his Metaphysica, sums up the Pythagorean’s attitude towards numbers The (Pythagoreans were) … the first to take up mathematics … (and) thought its principles were the principles of all things. Since, of these principles, numbers … are the first, … in numbers they seemed to see many resemblances to things that exist … more than [just] air, fire and earth and water, (but things such as) justice, soul, reason, opportunity
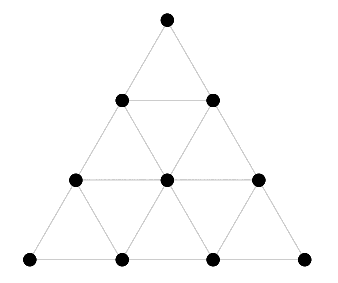
One of fascinating ancient discoveries is Tetractys. It is a symbol composed of ten dots in an upward-pointing triangular formation. It was a sacred pattern for the school of philosophers who followed the teachings of the Greek sage Pythagoras Tetractys itself can be interpreted as the symbolic blueprint of creation. Its image is an equilateral triangle based on the essential numbers 1 (top), 2, 3 and 4 (base), whose sum is the “perfect” number 10 ( 1 + 2 + 3 + 4 = 10) These numbers were considered by the Pythagoreans to be holy and at the origins of the universe. They believed that a four-fold pattern permeated the natural world, examples of which are the point, line, surface and solid and the four elements Earth, Water, Air and Fire. Musically they represent the perfect consonants: the unison, the octave, the fifth and the fourth. The importance of the tetractys to the Pythagoreans is illustrated by their oath of fellowship: I swear by the discoverer of the Tetractys, Which is the spring of all our wisdom, The perennial fount and root of Nature
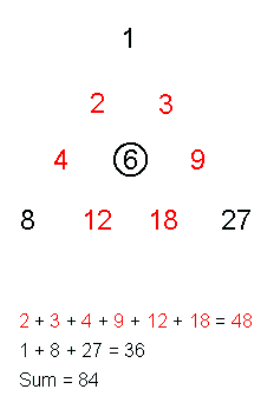
Tetractys generates hexagon which is 2-D projection of 3-D cube One particular triangular number that they especially liked was the number ten. It was called a Tetractys, meaning a set of four things, a word attributed to the Greek Mathematician and astronomer Theon (c. 100 CE). The Pythagoreans identified ten such sets In Plato’s Timaeus, we find that God created the Cosmic Soul using two mathematical strips of 1, 2, 4, 8 and 1, 3, 9, 27. These two strips have the shape of an inverted “V” or the “Platonic Lambda” since it resembles the shape of the 11th letter of the Greek alphabet “Lambda” (?).
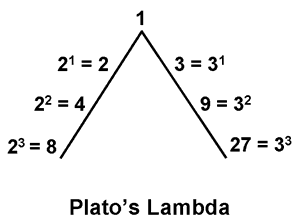
The Platonic Lambda interestingly describes 3 dimensional space:
Top – 1 — single point
1st row: 2 – 3 — linear dimension
2nd row: 4 – 9 — surface (2-D: 2×2 and 3×3)
3rd row: 8 – 27 — cubic volume (3-D: 2x2x2 and 3x3x3)
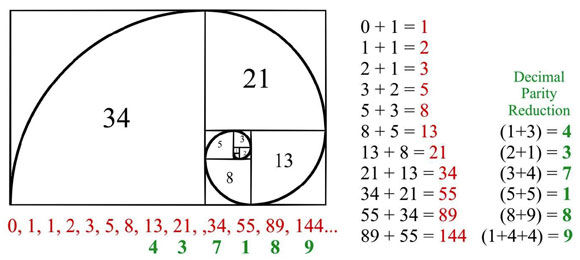
The Summation Series (Fibonacci): The natural progression follows a “summation series” that is known today as the “Fibonacci Series“ [ of course this Series was in existence before Fibonacci (born in 1179 CE) – he simply “re-discovered” it.] The Summation Series is a progressive series, where you start with the first two numbers, then you add their total to generate the next number, and so on. By definition, the first two Fibonacci numbers are 0 and 1, and each subsequent number is the sum of the previous two. The first summation progression: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, … It is worth to note that the first summation (Fibonacci) progression generates approximation of the golden ratio (PHI): 3/2 =1.5000 5/3 =1.666… 8/5 =1.6000 13/8 =1.6250 21/13=1.6154… 34/21=1.6190… 55/34=1.6176… 89/55=1.61818… 144/89=1.618…. The second of Fibonacci progression (provides approximate geometry of the pentagram and also lead to golden ratio ‘phi’ just like in the above example: 322/199=1.618… ): 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, … The Summation Series is reflected throughout nature. The number of seeds in a sunflower, the petals of any flower, the arrangement of pine cones, the growth of a nautilus shell, etc…all follow the same pattern of these series The overwhelming evidence indicates that the Summation Series was known to the Ancient Egyptians. Throughout the history of Ancient Egypt, temples and tombs (including pyramids) show in their design expression of the Summation Series: 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, . . .
Polygonal Numbers: A figurate number, also known as a figural number, is a number that can be represented by a regular geometrical arrangement of equally spaced points. If the arrangement forms a regular polygon, the number is called a polygonal number. The polygonal numbers illustrated above are called triangular, square, pentagonal, and hexagonal numbers, respectively
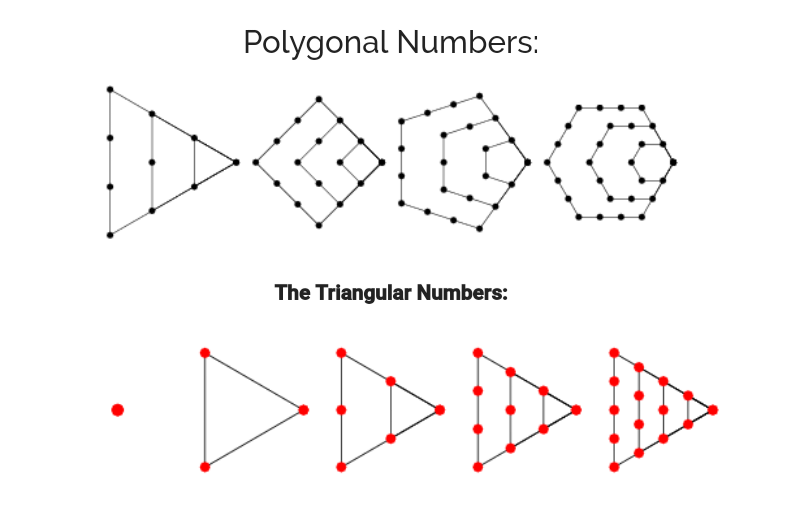
The triangular number Tn is a “figurate number” (a number that can be represented by a regular geometrical arrangement of equally spaced points) that can be represented in the form of a triangular grid of points where the first row contains a single element and each subsequent row contains one more element than the previous one. This is illustrated above for T1=1, T2=3, …. The triangular numbers are therefore 1, 1+2, 1+2+3, 1+2+3+4, …, so for n=1, 2, …, the first few are 1, 3, 6, 10, 15, 21, … Flower of Life and Figural Numbers:
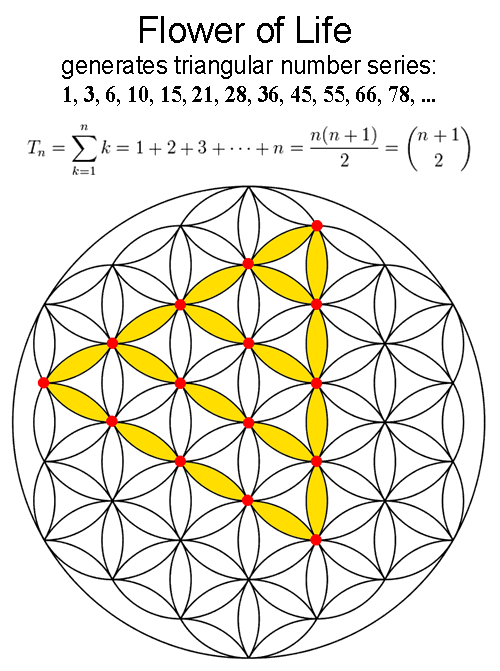

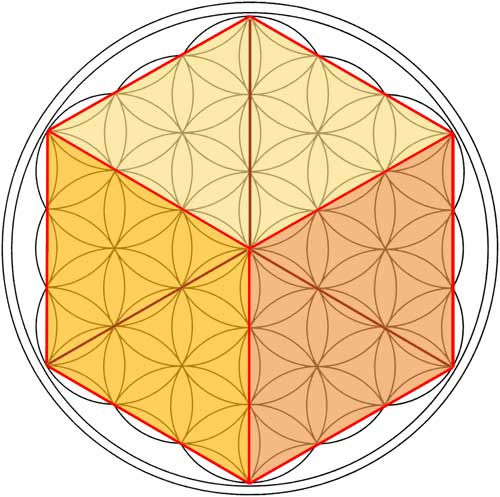
2-D projection of the Cube can be found in the Flower of Life
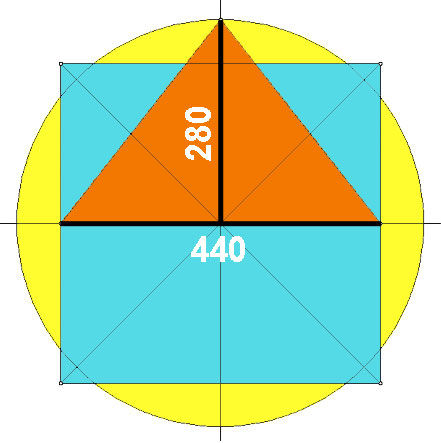
Principle of the Great Pyramid design (image above) based on the “squared circle” with “Pi” as 22/7
Patterns in Numbers and Pascal’s Triangle :
In mathematics, Pascal’s triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal. It is known as Pascal’s triangle in much of the Western world, although other mathematicians studied it centuries before him in India, Persia, China, Germany, and Italy.
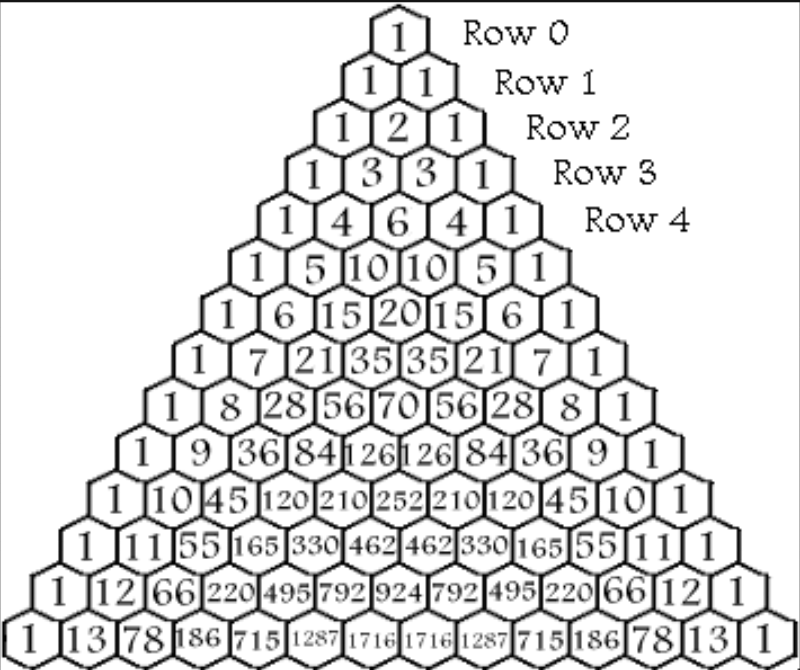
The rows of Pascal’s triangle are conventionally enumerated starting with row n = 0 at the top. The entries in each row are numbered from the left beginning with k = 0 and are usually staggered relative to the numbers in the adjacent rows. A simple construction of the triangle proceeds in the following manner. On row 0, write only the number 1. Then, to construct the elements of following rows, add the number directly above and to the left with the number directly above and to the right to find the new value. If either the number to the right or left is not present, substitute a zero in its place. For example, the first number in the first row is 0 + 1 = 1, whereas the numbers 1 and 3 in the third row are added to produce the number 4 in the fourth row.
The set of numbers that form Pascal’s triangle were well known before Pascal. However, Pascal developed many applications of it and was the first one to organize all the information together in his treatise, Traité du triangle arithmétique (1653).
The numbers originally arose from Hindu studies of combinatorics and binomial numbers and the Greeks’ study of figurate numbers
The earliest explicit depictions of a triangle of binomial coefficients occur in the 10th century in commentaries on the Chandas Shastra, an Ancient Indian book on Sanskrit prosody written by Pingala in or before the 2nd century BC. While Pingala’s work only survives in fragments, the commentator Halayudha, around 975, used the triangle to explain obscure references to Meru-prastaara, the “Staircase of Mount Meru”. It was also realised that the shallow diagonals of the triangle sum to the Fibonacci numbers. In 1068, four columns of the first sixteen rows were given by the mathematician Bhattotpala, who realized the combinatorial significance
At around the same time, it was discussed in Persia (Iran) by the Persian mathematician, Al-Karaji (953–1029). It was later repeated by the Persian poet-astronomer-mathematician Omar Khayyám (1048–1131); thus the triangle is referred to as the Khayyam triangle in Iran. Several theorems related to the triangle were known, including the binomial theorem. Khayyam used a method of finding nth roots based on the binomial expansion, and therefore on the binomial coefficients
In 13th century, Yang Hui (1238–1298) presented the arithmetic triangle that is the same as Pascal’s triangle. Pascal’s triangle is called Yang Hui’s triangle in China. The “Yang Hui’s triangle” was known in China in the early 11th century by the Chinese mathematician Jia Xian (1010-1070).
In Italy, it is referred to as Tartaglia’s triangle, named for the Italian algebraist Niccolò Fontana Tartaglia (1500–77). Tartaglia is credited with the general formula for solving cubic polynomials, (which may in fact be from Scipione del Ferro but was published by Gerolamo Cardano 1545).

Blaise Pascal’s version of the triangle
Pascal’s triangle has many amazing properties and contains many “special” patterns of numbers. Below we are presenting few of the most incredible examples
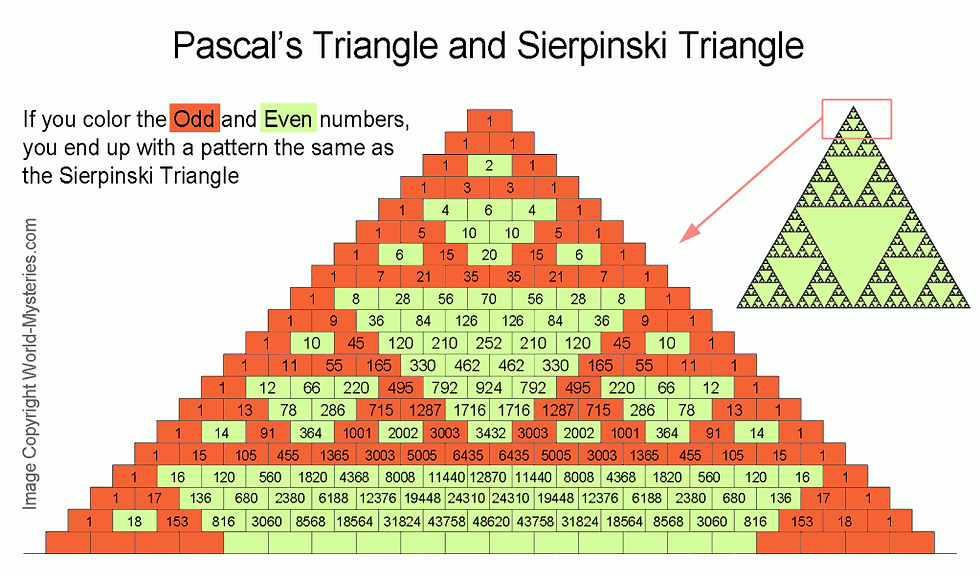
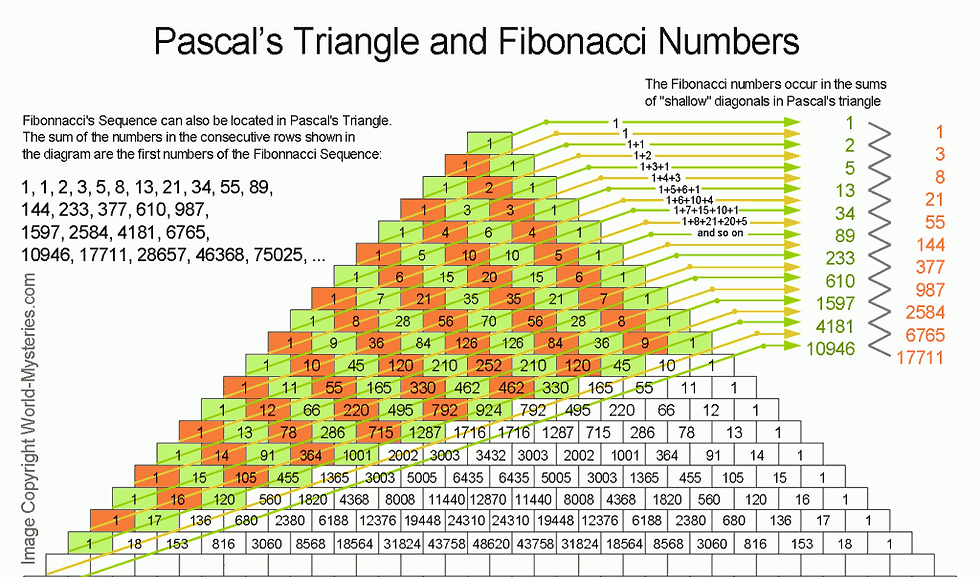
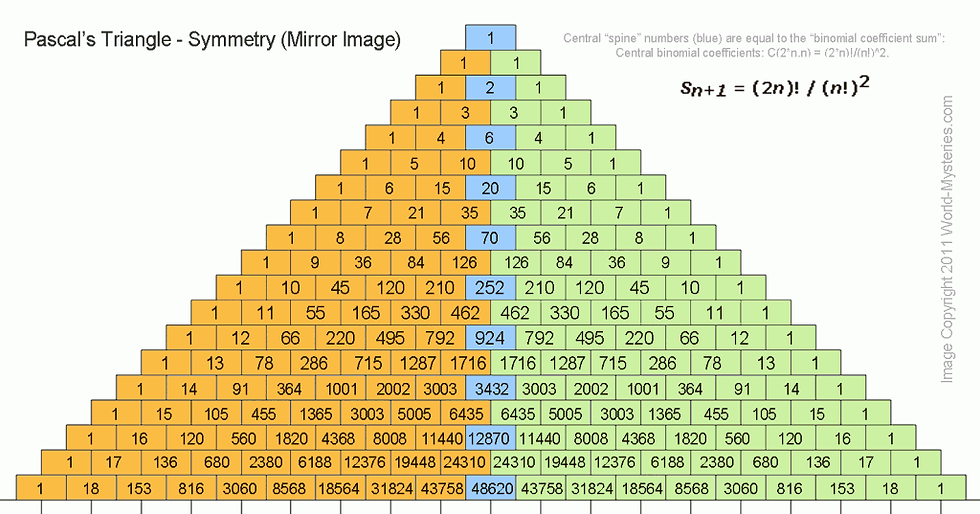
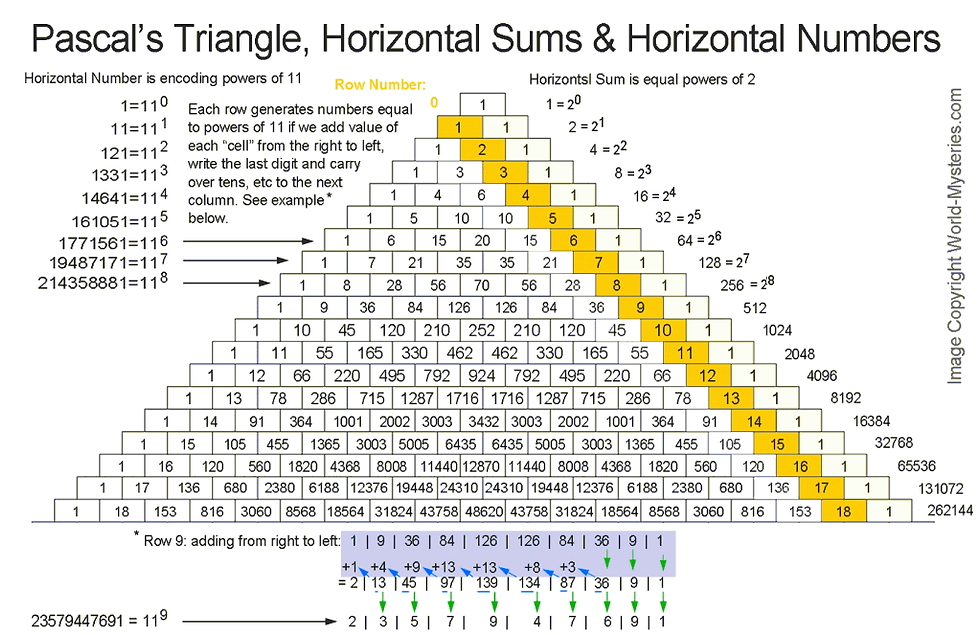
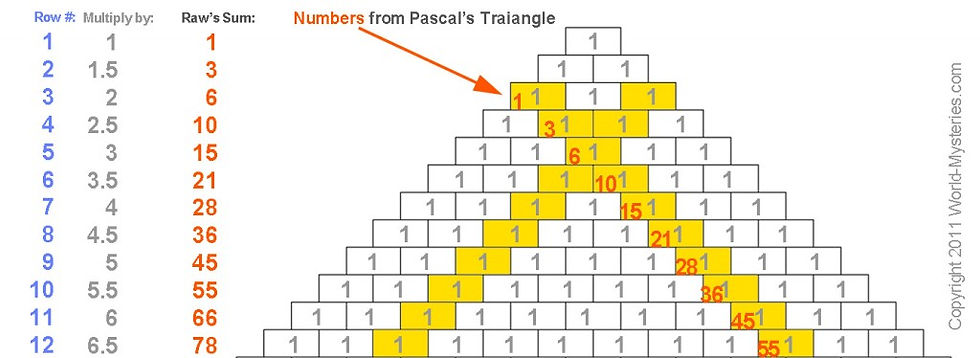
The Fibonacci series has a pattern that repeats every 24 numbers:
Numeric reduction is a technique used in analysis of numbers in which all the digits of a number are added together until only one digit remains. As an example, the numeric reduction of 256 is 4 because 2+5+6=13 and 1+3=4.
Applying numeric reduction to the Fibonacci series produces an infinite series of 24 repeating digits:
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9
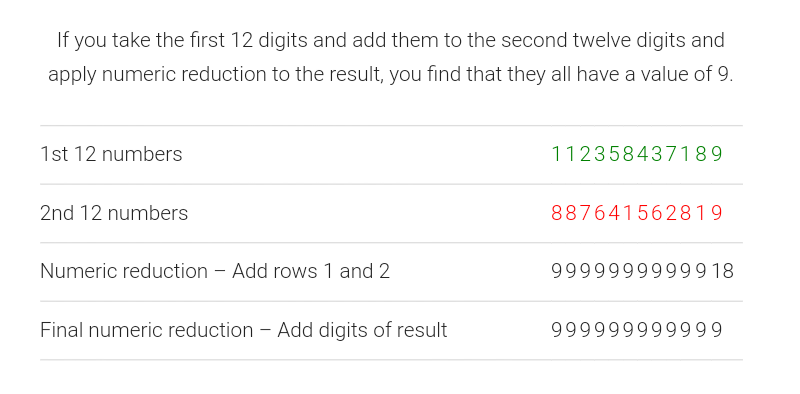
Phi and its counterpart Phee are deemed the Golden Mean, the Golden Proportion and the Golden Ratio. This ratio is the number 1.618 and is the number upon which all of nature performs her balancing act.
Phi was not just some arbitrary number or ratio somehow manifested through mindless chaotic universal construction but a key to unlock the door to certain universal truths within the sacredness of the Heavens and Earth.
We can find the Golden Ratio within the Fibonacci Sequence:
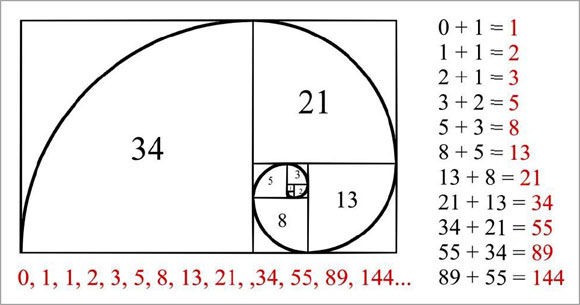
taking a number later in the sequence and dividing it by its predecessor we can find our holy ratio of 1.618. Example: 144 / 89 = 1.618
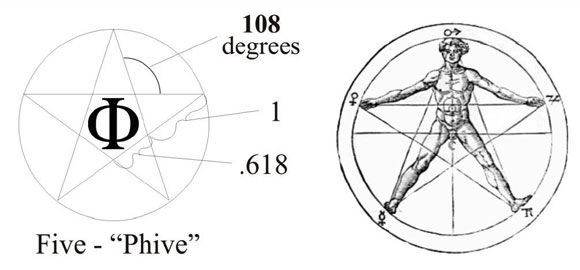
We are going to find this Holy 108 within the spiraling unfolding Fibonacci sequence
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1
1 + 1 + 2 + 3 + 5 + 8 + 4 + 3 + 7 + 1 + 8 + 9 + 8 + 8 + 7 + 6 + 4 + 1 + 5 + 6 + 2 + 8 + 1 = 108
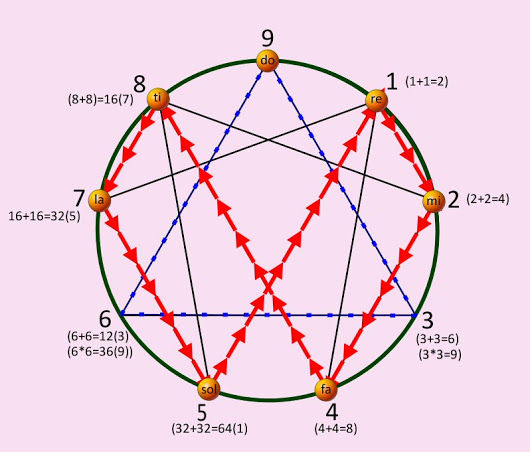
At this point some of you might be thinking, “What in the world do these number patterns have to do with real world applications?” These number groupings piece together into a jig-saw-like puzzle pattern that perfectly demonstrates the way energy flows. Our base-ten decimal system is not man made, rather it is created by this flow of energy. Amazingly, after twenty years of working with this symbol and collaborating with engineers and scientists, Marko discovered that the 1,2,4,8,7,5 was a doubling circuit for a very efficient electrical coil. There was still one more very important number pattern to be realized. On the MATHEMATICAL FINGER PRINT OF GOD notice how the 3, 9, and 6 is in red and does not connect at the base. That is because it is a vector. The 1,2,4,8,7,5 is the third dimension while the oscillation between the 3 and 6 demonstrates the fourth dimension, which is the higher dimensional magnetic field of an electrical coil. The 3, 9, and 6 always occur together with the 9 as the control. In fact, the Yin/Yang is not a duality but rather a trinary. This is because the 3 and 6 represent each side of the Yin/Yang and the 9 is the “S” curve between them. Everything is based on thirds. We think that the universe is based on dualities because we see the effects not the cause


Phi(1.618) geometrys:

Number 666:
108×2= 216 = 6×6×6 , 666 is the number of the Sun
108 has 12 divisors: 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108
The number 666 has 12 divisors {1, 2, 3, 6, 9, 18, 37, 74, 111, 222, 333, 666}
Sentence from the Bible: YHVH Shemesh or “The Lord is the Sun”.YHVH = yod + heh + vau + he = 10 + 5 + 6 + 5 = 26 Shemesh = shin + mem + shin = 300 + 40 + 300 = 640 26 + 640 = 666
Perfect cube numbers: 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728 The 6th number is 216 or 6 x 6 x 6 and 6th sphere on the Tree of Life is Sun or Tiphareth on Hebrew. 37th triangular number is 666. 3 + 7 = 10 or tetraktys, Tree of Life.
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20+21+22+23+24+25+26+27+28+29+30+31+32+33+34+35+36=666
Number 666 in binary is 1010011010, which contains 10 digits, or first ten Ideas in Universal Mind, the Tree of Life
If we add up all numbers from 1-36 it will result in 666. 36 is sacred Pythagorean number of Sun
Number 216 or 6 x 6 x 6 is also produced of 3 x 3 x 3 + 4 x 4 x 4 + 5 x 5 x 5, the cubical number of perfect Pythagorean triangle c2 = a2 + b2. These ratios of 3:4:5 is ancient Egyptian symbol for Trinity of Osiris, Isis and Horus
Link:
http://blog.world-mysteries.com/science/numbers-magick/








Comments